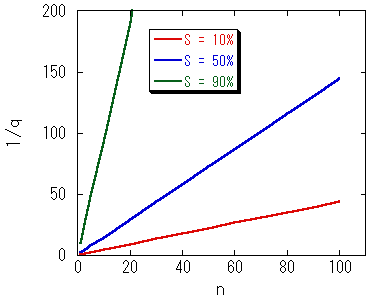
 (※)試行失敗率 q の逆数を,連続成功回数 n に対してプロットしてみると,
この図のように,ほぼ比例しています.すなわち q と n が反比例
(ただし n が 1 より小さいところではずれてくる).
これは,達成確率 S を何パーセントに設定しても同じです.
q と n が反比例することを解析的に示そうとしたんだけど,できてません.
(※)試行失敗率 q の逆数を,連続成功回数 n に対してプロットしてみると,
この図のように,ほぼ比例しています.すなわち q と n が反比例
(ただし n が 1 より小さいところではずれてくる).
これは,達成確率 S を何パーセントに設定しても同じです.
q と n が反比例することを解析的に示そうとしたんだけど,できてません.
2004-02-03
updated on 2006-02-02
技術習得系のスポーツで,あることにn回連続して成功するまで練習する なんてことをします.たとえばバスケットのフリースローを 10回続けて入れるとか, ピッチャーが 10球連続してストライクを投げるとか,けん玉の剣に 20回続けて挿すとか, サッカーのリフティング 100回とか. 一回一回の成功確率(たとえば一投のフリースローが入る確率)と, 何回連続して成功するかということとの関係をちょっと考えてみました.
どんなに下手でも,年がら年中フリースローを投げつづけていれば, いつしか10回連続成功なんてこともあるでしょう. どんな確率で「連続成功」を達成するかも考えないと,技術の確実性の評価はできません. そこで,「n回連続成功」に何度も挑戦したときの達成確率を3通り設定してみます.
(1 - q)n = S
すなわち
q = 1 - S1/n
となります.10回連続成功(n = 10) として q を計算してみます. ついでに 1-q (個々の試行の成功確率)も.
| 10回連続成功の達成確率 (%) | 個々の試行の失敗率 q (%) | 個々の試行の成功率 1 - q (%) |
| 10 | 20.57 | 79.43 |
| 50 | 6.70 | 93.30 |
| 90 | 1.05 | 98.95 |
この結果を見ると,
| 20回連続成功の達成確率 (%) | 個々の試行の失敗率 q (%) | 個々の試行の成功率 1 - q (%) |
| 10 | 10.87 | 89.13 |
| 50 | 3.41 | 96.59 |
| 90 | 0.53 | 99.47 |
20回連続でできる人は,10回連続でできる人よりも,失敗率でいったらおよそ 半分ぐらいだということが分かります. また,ほぼいつでも20回連続フリースローを決めてみせてくれる人(Q = 90%)は, フリースロー失敗率がわずかに0.53%,200本打って1本はずすだけという正確性を 持っていることが分かります.
さらに100回連続成功の場合を計算してみます.
| 100回連続成功の達成確率 (%) | 個々の試行の失敗率 q (%) | 個々の試行の成功率 1 - q (%) |
| 10 | 2.28 | 97.72 |
| 50 | 0.69 | 99.31 |
| 90 | 0.11 | 99.89 |
10回連続成功の場合と比べると,個々の試行の失敗率がほぼ 10分の1ですね. 連続成功の達成確率 S をいくつに設定するかにかかわらず, 連続成功回数は,個々の試行の失敗確率にほぼ反比例します. 連続成功回数を K倍に伸ばすには,失敗確率を 1/K にまで下げる必要がある ということです(※).
また,たまに 100回連続成功を達成できる(達成率 10%)って人は,達成率 90% で 安定して 10回連続成功をやってみせる人よりも,個々の試行の失敗率は2倍も大きい (1.05% に対して 2.28%)ことも分かります. 粘りに粘った末の連続成功記録は,すくなくとも技術の正確性という観点からは, あんまり威張れないようです.
 (※)試行失敗率 q の逆数を,連続成功回数 n に対してプロットしてみると,
この図のように,ほぼ比例しています.すなわち q と n が反比例
(ただし n が 1 より小さいところではずれてくる).
これは,達成確率 S を何パーセントに設定しても同じです.
q と n が反比例することを解析的に示そうとしたんだけど,できてません.
(※)試行失敗率 q の逆数を,連続成功回数 n に対してプロットしてみると,
この図のように,ほぼ比例しています.すなわち q と n が反比例
(ただし n が 1 より小さいところではずれてくる).
これは,達成確率 S を何パーセントに設定しても同じです.
q と n が反比例することを解析的に示そうとしたんだけど,できてません.
(追記 2006-02-02)このページを書いたことも忘れてしまったころになって,九州大学の 粕谷英一さんからメールをいただきました. q と n が反比例することについてです. (1 - q)n = S の両辺の対数をとってから Taylor 展開すれば一発だとのこと. q (失敗確率)がじゅうぶんに小さければ,q の一次の項だけとって nq = -log(S) から, Sが所与なら n と q は反比例する.なるほど. ご教示ありがとうございました.