Updated on 12 April 2002
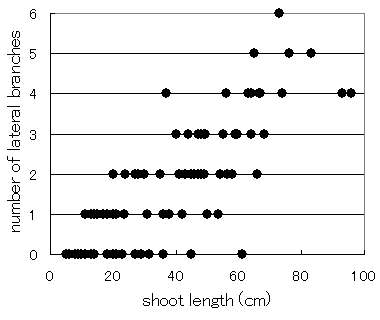
下の図は,1年間に伸びた枝の長さと,そこから枝分かれしている 側枝の数の関係です. 主軸からの一次枝の分枝と, 一次枝からの二次側枝の分枝とは区別して扱います. この図は,主軸のデータだけ,85個のデータをプロットしてあります.

両者のあいだに正の相関関係がありそうなことは一見して分かりますが, 有意な相関があることを示したいだけじゃなくて, この関係をシミュレーションモデルの中に組み込むことを考えています. このデータをどうモデル化したものか.
まず考えられるのは,枝の長さに応じて側枝数を決めるなんらかの関数を 使うことです(たとえば 側枝数 = a x 枝長 + b みたいに). でも,これでは同じ枝長でも側枝数がかなりばらつくことは表現できません. 短い枝からも低い頻度で側枝がでるという現象や, 長い枝でも側枝がないことがあるという現象を切り捨てたくはないので, 回帰式をひとつ求めて推定というやりかたはまずい.
そこで考えたのが,枝の長さに応じて,ある本数の側枝がでる確率に注目する という手です. まず,関数 P(x, n) を定義します.これは,長さが x の枝から n本以下の側枝が でる確率を与えます. ちょうどn本の側枝がでる確率は,
ちょうど n本の側枝がでる確率そのものをデータから推定すると, 全部の場合を足したときにちょうど100%になるように調整するのが面倒そうです. その面倒を避けて,n本以下の場合の確率を使っています.
P(x, n)の形としてはこんなものを考えました.
P(x, n) = an / (x^bn + an)
x^bnは,xの bn乗の意味です. パラメータ aと bは枝の本数 nごとに決めるので,添え字のnを付けてあります.
あとは,このパラメータの値の決め方です. 当然,もっともよく観測データと合うように決めたい. となると最尤法の出番でしょうか. あいにく,わたしは今まで最尤法を使った経験はありません.でも, 「困ったときはネットに聞け」とも,「頼みの網(ネット)」とも言います. 久保拓弥さんの 尤度を使った推定法あれこれ のページに掲載されている 「区画」をとらない「率」推定(最初の一歩篇) (PDF, 320KB) では,生態学者に身近な例を題材に,最尤法の初歩が要領よく説明されています. まずはこれを勉強してみることにしました.
最尤法によるパラメータ推定の基本は,データの推定値と観測データとの合致の 度合を表す尤度が最大になるパラメータを探すことです.そのためには, 尤度をパラメータで微分したものがゼロになるところを探せばよいのですが, 解析的には求まらないのがふつうのようです. 久保さんのテキストでは,多次元のNewton-Raphson法を使ってパラメータの 最尤推定をする方法が紹介されています.
そこまで勉強するのは大変そうなので,とりあえずは愚直にパラメータを 動かしながら尤度が最大になるところを探すことにしました. aと bふたつのパラメータのうちまずは a を固定しておき,b を動かして 尤度が最大になるところを探す,次に b をそこに固定しながら a を 動かして尤度が最大になるところを探す,という作業を繰り返します. a,bがじゅうぶんに収束してきたら探索を終了します.
尤度は以下のような手順で計算してみました.
枝の長さを x として,その時に側枝の数が n 本以下である確率 pは p = a / (x^b + a) となります.もし観測データの側枝の数が n以下だったら,確率 pの 事象が起きたことになるし,側枝の数が nより大きかったら 確率 1- pの事象が起きたことになります. この確率を全部の測定データについて求めて掛け合わせたものが尤度です. ただし,1より小さい数をどんどん掛けていくとすごく小さい値になって いくので,まず対数をとってから足し算して,対数尤度を求めるのが ふつうのようです.
対数尤度の値は,当然 aやbの値によって変化します.尤度が最大になる a と bの値を探すことで,観測されたようなデータが得られる可能性が 最大になるような,すなわちもっとも観測データとよく合うパラメータを 見つけることができます.
尤度が最大になるところを探すアルゴリズムを工夫しつつ, Ruby でプログラムを書いてみました(プログラムはきれいにしてから載せる予定). 下の表が推定したパラメータです.
| n | an | bn |
|---|---|---|
| 0 | 8.401e+002 | 2.39 |
| 1 | 2.527e+005 | 3.59 |
| 2 | 2.317e+009 | 5.47 |
| 3 | 1.326e+012 | 6.63 |
| 4 | 1.928e+01 | 5.72 |
| 5 | 1.081e+010 | 4.66 |
最大で6本まで側枝を持つものがあるので,P(x, 5)まで求めてあります. 6本の側枝がでる確率は1 - P(x, 5) です. 推定したパラメータを使って,P(x, n)の形を描いてみました.
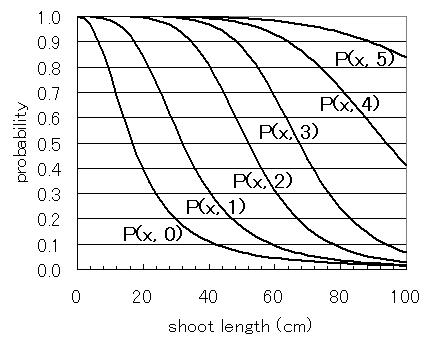
たとえば長さ40センチの枝の場合,1本も側枝がない確率が10%程度, 1本だけ側枝がある確率が20%,2本の側枝がある確率が一番高くて50%程度, というように読み取れます.
85個のデータを説明するのに, P(x, 0) からP(x, 5) までそれぞれ2個ずつのパラメータ,全部で12個のパラメータ を動員してますから,これで観測データが再現できなかったらがっかりです. 測定された枝長データを使っておそるおそる側枝の本数を計算してみました.
P(x, n)で与えられるのは確率だけですから,実際に何本の側枝を持つかは 乱数で決めます.4回の試行を行った結果が下の図です.
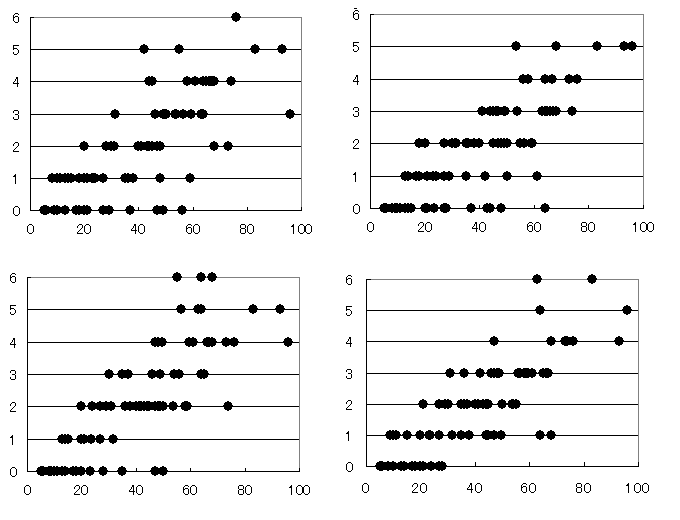
観測データ と,こわいほど似ているような気がするのですが,いかがでしょうか.
今後の課題は,
などです.
このページの内容に,久保拓弥さんからコメントをいただきました.
側枝の数が n本以下である確率を与える P(x, n) を,nの値それぞれについて
独立に最尤推定した場合(これが私が試みた方法)と,
側枝の数が ちょうどn本である確率を与える P(x, n) - P(x, n-1) に
注目して n のすべての値についていっぺんに最尤推定するというやりかたで
求まる解は同じだろうか,という指摘です.
久保さんにいろいろ教えていただきながら検討してみましたが,
P(x, n) がxに依存しない形の場合ならば同じ解が求まることが証明できる,
xに依存する形の場合も,たぶん大丈夫なんでないかな…というところで
止まってます.
補遺
Magnoloid Top Page |
| Top Page |