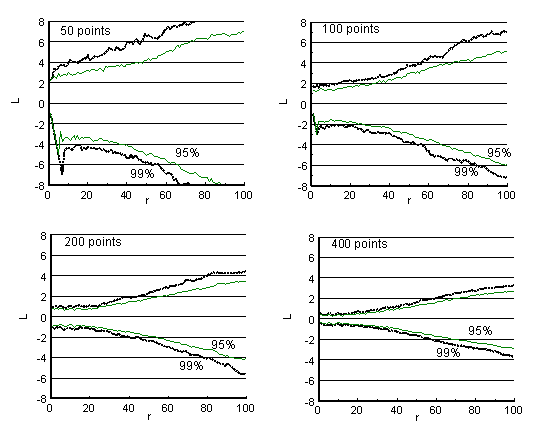
200メートル四方の面にランダムに点をばらいて,L関数の値を計算しました. 1,000回の試行を行って,その結果をもとに,距離r(横軸)に対応するL関数の 値の99%信頼区間(黒の点線)と95%信頼区間(緑の実線)を求めました.
つまり,点の散布がまったくランダムに起こったとしても,L関数の値は ぴったりゼロになるわけではなく,緑の線の内側の範囲で揺らぐのは ありがちなことだ,測定データから求めたL関数の値が緑の線の外側に来たら, 点の散布プロセスはランダムではないと5%の危険率(第一種の過誤の確率) で結論できる,ということになります.
点の個数は50個から400個まで試してみました.当然ながら, 点の数が大きくなるほど信頼区間が狭くなっていくことが分かります. 測定点が多いほど,ランダム分布からのずれを見いだす検出力が高まる (第二種の過誤の確率が小さくなる)ことになります.

ところで,実際に森林で木の位置を調べるとき,一本一本についてx-y座標を きっちりと決めていくのは大変です. 便法として,調査地を小区画に区切って,個々の木がどの区画に属するかだけ調べて, 区画内での正確な位置までは測らない,という方法があります. そのようなデータをもとにL関数を計算したらどうなるかを試してみました. 200メートル四方の面の中を,5メートル四方の小区画に区切り, 各小区画内の木はすべてその小区画の中心にいるものとして扱います. つまり,位置の解像度を5メートルにまで落として計算したことになります.
上の例と同様にランダムに点を分布させてL関数を計算する試行を1,000回 行って95%信頼区間を求め,正確な位置データに基づいて計算する場合と 比較してみました.赤い線が5メートル区画データを使って計算した場合, 緑の線が正確な位置データから計算した場合です.
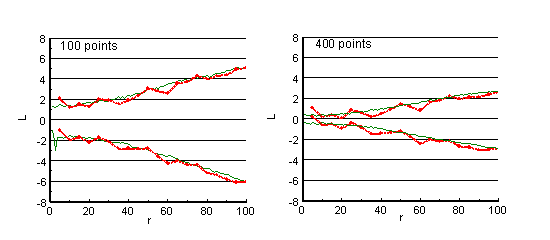
区画データを使った場合,位置が5メートルきざみであることを反映したと思われる 周期的な揺れがあらわれますが,全体として大きなずれはないようです. あとは,集中パターンや排他パターンを生成して,正確な位置を使う場合と 区画データにした場合との検出力を比較する必要がありますが,区画データも そこそこ使えそうです.
もちろん,5メートル区画のデータからは5メートル以下の空間スケールの 構造は調べようがありません.いっぽう,データ数は多いほどパターンの検出力 が高まるのは上で見たとおりです.解像度を落とすことで測定のスピードは 上がりますから,解像度と検出力のバランスを考えて,効率のよいデータの 取り方を選択するのがよいでしょう.