親枝と子枝の長さの関係をモデル化する（頂芽編）

since 10 May 2002
Updated on 15 May 2002

まず，子枝の長さと親枝の長さの関係をそのままプロットしてみました． 枝の次数によっても関係が違いそうなので， 一次枝だけ取り出して描いてあります．

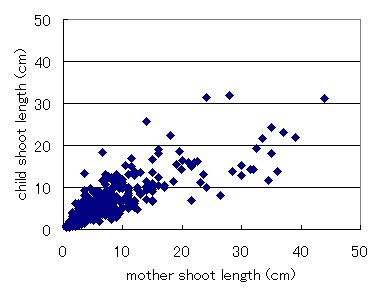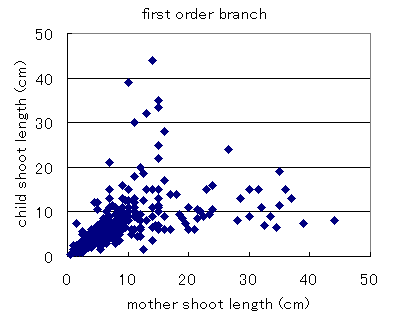
親枝が長いほど，その子枝も長いという全体的な傾向があるようです． ただ，ばらつきが大きくてそれ以上はよくわかりません．． 次に，子枝の長さと親枝の長さの比率を計算して，親枝長に対してプロット してみました．

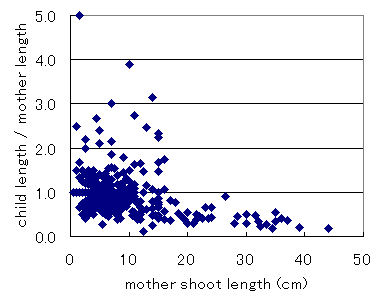
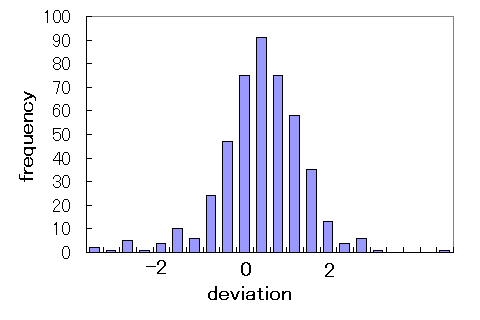
右肩さがりのパターンが見えてきました． つまり，親枝が長いほど，その子枝は親枝よりも短めということです． また，親枝長を固定して考えたときの，子枝長と親枝長の比率のばらつき具合は， どうも大きいほうに尾を引いた関係のように見えます． ためしに，長さの比率の対数をとって見ると，このようになります．

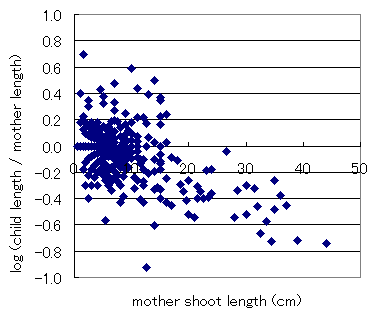
この関係をモデル化の出発点にしてみました． 以下では，親枝の長さをL，子枝長と親枝長の比の対数をQと書くことにします． 上の図の特徴としては，まず，Lが大きいほど，Q の平均値(Q_mean)が 小さいことがあげられます．それに加えて，Lが大きいほどQ のバラツキが小さい ような気もします． LとQ_meanの関係を直線的だと仮定するのはどうも無理が ありそうなので，パラメータの数が増えて面倒だけど，

Q_mean(L) = c0 /(L + c1) - c2　　…式(1)

で表現することにします．c0, c1, c2は定数です．

次に，Qのバラツキです．ばらつき方は，いちおう正規分布に従うということに しておきます．この点についてはあとで少し吟味します． Qのバラツキの標準偏差 Q_sdは

Q_sd(L) = c3 /(L + c4)　　…式(2)

で表現することにします． 式(1),(2)の５つのパラメータの値を，最尤法で推定することにします． 最尤法については 前のページ で簡単に触れました．

５つのパラメータを動かしながら一番もっともらしい値の組みを探すのは けっこう時間がかかります（私の書いたプログラムのアルゴリズムが あまりに愚直なもんで）が，ともかくお茶を（うんとゆっくり）飲んで待ってれば 結果が出てくる程度の時間で済みました． パラメータの値は以下のようになりました．

これらのパラメータを使って，子枝の長さを求めてみます． 最初に示したデータセットの親枝の長さを入力として与え， 対応する子枝の長さを計算します． log(子枝長/親枝長)の平均値は式(1)で決まります． あとは，式(2)で計算した標準偏差をもとに，乱数を使って log(親枝長/子枝長)を決め，子枝の長さを計算します． そうやって求めた親枝長と子枝長の関係の一例を示します．

測定データ と比べると，おおよその雰囲気はよさそうですが，親枝に対して極端に 長い子枝が生じるところは表現できてません．また，親枝が短いところで 子枝長のバラツキが大きめに見えています． この原因としては，

1. 最尤推定をする時，平均値の推定のずれを吸収するためにバラツキが 大きめに見積もられた．
2. log(子枝長/親枝長)のばらつき具合が正規分布ではない．

式(1)が log(子枝長/親枝長) の親長依存性を表現するのにかならずしも ピッタリではないだろうから，1の理由は多かれ少なかれありそうです．

2の可能性を検討するために，もとのデータについて期待値からのずれ具合の分布を 見てみます．（親枝長，子枝長）の対のデータそれぞれについて， 親枝長をもとに式（１）でlog(子枝長/親枝長)の期待値を求めます． これと，測定データから計算した log(子枝長/親枝長)の値との差を求めます． さらに，この差を式（２）で求めた標準偏差で割ります． こうして正規化したずれ具合のヒストグラムを書いてみます． さて，当初の仮定通りに正規分布と見てよいでしょうか？

ぱっと見た形としてはとてもそれらしいのですが，ピークが０よりもやや大きく， 分布の裾はマイナス側がやや大きめです（きちんと検定はしてませんが）． 平均値からのずれが正規分布ではない，という要素もいくらかはありそうです．

でも，樹形の再構成のためにはこんな程度できっと充分でしょう． まずはよしとしておきます．